Mineral Nutrition of Plants
SoilScience/Botany/Horticulture 626
Phillip Barak and Edgar Spalding, Instructors
University of Wisconsin-Madison
Fall 2000
Fitting Michaelis-Menten parameters to nutrient uptake data
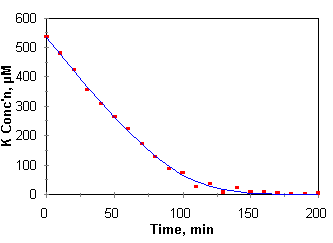
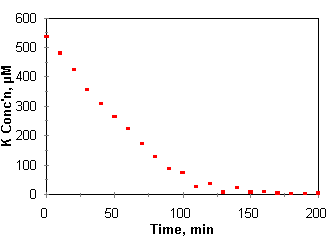 One
of the more interesting methods of generating nutrient uptake data is the
nutrient draw down method of Claasen and Barber (1973). By this method, growing
plants are placed in a limited volume of nutrient solution and are allowed to
draw down the nutrient concentrations over a short period of time. Aliquots are
removed and analyzed for concentrations of the nutrient or nutrients of
interest. In a simple case, volume changes due to evapotranspiration and
quantities of nutrients withdrawn with the aliquots are small to the point of
being negligible. The slope of concentration (or quantity) with respect to time
is the rate of nutrient uptake, dC/dt, and the rate of nutrient uptake can be
measured for a range of concentrations in a single experiment as the nutrient
concentration is drawn down by plant uptake. One
of the more interesting methods of generating nutrient uptake data is the
nutrient draw down method of Claasen and Barber (1973). By this method, growing
plants are placed in a limited volume of nutrient solution and are allowed to
draw down the nutrient concentrations over a short period of time. Aliquots are
removed and analyzed for concentrations of the nutrient or nutrients of
interest. In a simple case, volume changes due to evapotranspiration and
quantities of nutrients withdrawn with the aliquots are small to the point of
being negligible. The slope of concentration (or quantity) with respect to time
is the rate of nutrient uptake, dC/dt, and the rate of nutrient uptake can be
measured for a range of concentrations in a single experiment as the nutrient
concentration is drawn down by plant uptake. |
Assuming Michaelis-Menten kinetics, dC/dt = (1/Vol)
vmaxC/(Km+C), to be generally applicable to
this problem, the issue divides into two problems: 1) expressing
Michaelis-Menten kinetics, a derivative equation, in integral form as a
function of time, and 2) parameter optimization of vmax and
Km to generate the best fit of the kinetic model to the
experimental data.
1) Integration: The Michaelis-Menten equation may be
analytically integrated to give an expression explicit in C but not in t. This
means that if C is measured, then with values of vmax,
Km, and C0, the time t predicted by the
Michaelis-Menten kinetic model to draw down concentrations to that value of C
can be calculated. In practice, one typically measures a value of C at an
interval of t, not the other way around, so this information is not as useful
as it may seem.
Alternatively, the Michaelis-Menten equation can be numerically
integrated. The simplest approach uses Euler's method:
Ci+1=Ci + dCi/dt
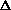 t. Inspection shows
that this approach to numerical integration simply ties together a number of
straight line segments. The slope at the beginning of each segment is correct,
but that slope is not altered until the end of the segment. Error is cumulative
and the only recourse is to reduce the size of
t. Inspection shows
that this approach to numerical integration simply ties together a number of
straight line segments. The slope at the beginning of each segment is correct,
but that slope is not altered until the end of the segment. Error is cumulative
and the only recourse is to reduce the size of
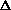 t and recalculate
dCi/dt more frequently. How often is enough? Hard to say in advance.
Fortunately there are better, if slightly less intuitive, methods.
t and recalculate
dCi/dt more frequently. How often is enough? Hard to say in advance.
Fortunately there are better, if slightly less intuitive, methods.
The Runge-Kutta algorithm makes four evaluations of dC/dt
between each time step, which are combined to create a single step. The overall
accuracy is much better than taking four smaller steps. The first evaluation is
identical to Euler's method. The second and third use the previous step to
evaluate dC/dt at the middle of the time step, and the fourth evaluation uses
the third at the end of the time step. The four evaluations are weighted and
used to create a single step from i to i+1. The equations are:
k1 =
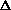 t dCi/dt
t dCi/dt
k2 = 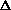 t d(C+k1/2)/dt
t d(C+k1/2)/dt
k3 =
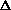 t
d(C+k2/2)/dt
t
d(C+k2/2)/dt
k4 =
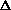 t
d(C+k3)/dt
t
d(C+k3)/dt
Ci+1 = Ci + k1/6 + k2/3+
k3/3 +k4/6
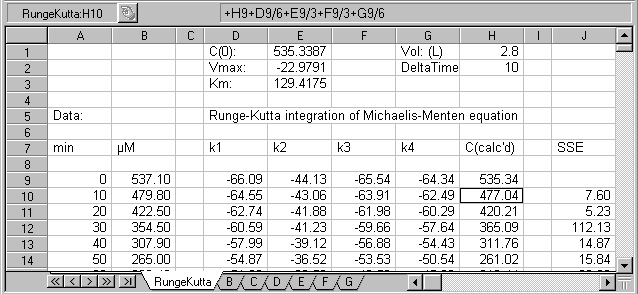
These equations may rather simply incorporated into spreadsheet format,
permitting evaluation of C as a function of time, given a set of values for
vmax, Km, and C0. Additional
time steps may be required on occasion if the behavior of the function is too
abrupt, although this is not likely the case for Michaelis-Menton kinetics.
2) Parameter Optimization: Obviously, there are too
many choices for vmax, Km, and
C0 to sort through manually when trying to fit a model to real data.
An obvious choice is to decide upon a figure-of-merit, a criterion of
goodness of fit, and then seek those values of the parameters that minimize
that figure-of-merit. Least squares of the residuals, or minimizing the sum of
squared differences between predicted and measured values, is long established
as acceptable and is often termed SSE, sum of the squares of the errors.
 Numerous parameter optimization schemes are known and
computer code is available from Numerical Recipes. Alternatively,
spreadsheets contain such code in the "Optimizer" feature of QuattroPro and the
"Solver" add-in of Excel, and the details of algorithm are not important.
Once the Michaelis-Menten model has been written with a given
set of vmax, Km, and C0 values,
predicted values may be compared to measured values to calculate SSE, and then
Optimizer/Solver may be used to search for and find values of
vmax, Km, and C0 that minimize
SSE. Parameter optimization typically proceeds until either a preset number of
iterations has been completed or continued iterations do not improve the
overall fit by a preset value. The beauty of parameter optimization is that the
initial guesses for the parameter values affect the path of the parameter
search but not the outcome (unless there is a degenerate situation in which the
parameter makes no difference at all in the model.) Sometimes there is need to
constrain values of the parameters to ensure their logical meaning; for
example, Km and C0 must be positive. Numerous parameter optimization schemes are known and
computer code is available from Numerical Recipes. Alternatively,
spreadsheets contain such code in the "Optimizer" feature of QuattroPro and the
"Solver" add-in of Excel, and the details of algorithm are not important.
Once the Michaelis-Menten model has been written with a given
set of vmax, Km, and C0 values,
predicted values may be compared to measured values to calculate SSE, and then
Optimizer/Solver may be used to search for and find values of
vmax, Km, and C0 that minimize
SSE. Parameter optimization typically proceeds until either a preset number of
iterations has been completed or continued iterations do not improve the
overall fit by a preset value. The beauty of parameter optimization is that the
initial guesses for the parameter values affect the path of the parameter
search but not the outcome (unless there is a degenerate situation in which the
parameter makes no difference at all in the model.) Sometimes there is need to
constrain values of the parameters to ensure their logical meaning; for
example, Km and C0 must be positive. |
There are yet more wrinkles to this story. One can use much the same
techniques to write spreadsheet entries that include removal of aliquots and
changes in volume due to evapotranspiration. Calculations can be written that
include Cmin, a concentration below which no nutrient uptake can
occur. Other kinetic models can be evaluated numerically as well, including
first and zero order kinetics.
A sample MS Excel spreadsheets can be downloaded: MS Excel v5/v7:
mmdemo.xls (uses Solver add-in; corrected and amended,
Oct 2002)
References:
A method for characterizing the relation between nutrient
concentration and flux into roots of intact plants. N. Classen and S.A. Barber.
1974. Plant Physiol. 54:564-568.
Chap 16: Integration of Ordinary Differential Equations: 16.1
Runge-Kutta Method (p 704; see also 16.2 Adaptive Stepsize Control for
Runge-Kutta p. 708); Chap 15: Modeling of Data: 15.1 Least Squares as a
Maximum Likelihood Estimator; 15.5 Nonlinear Models; 15.6 Confidence Limits on
Estimated Model Parameters. In: Numerical Recipes in Fortran 77
(2nd ed.) or Numerical Recipes in C (2nd ed.)
(see also
Numerical Recipes homepage)
Leonor Michaelis (b. Berlin, 1875; d. New York City, 1949).
Dictionary of Scientific Biography. Vol. 18 (Suppl. II):620-625.
A wonderful scientific biography of a scientist who worked out kinetic
laws of enzymes when the pH scale was less than 10 years old and when enzymes
would not be recognized as proteins for another 15 years! Maude Leonora Menten,
a visitor to his lab during the period that led to the 1913 paper that
established Michaelis-Menten kinetics, went on to become a distinguished
pathologist.
This page was last modified by
Phillip Barak, Univ. of
Wisconsin, on 1 Oct 2002. All rights reserved. This material may not be
reposted on any server without express permission of the author.
 One
of the more interesting methods of generating nutrient uptake data is the
nutrient draw down method of Claasen and Barber (1973). By this method, growing
plants are placed in a limited volume of nutrient solution and are allowed to
draw down the nutrient concentrations over a short period of time. Aliquots are
removed and analyzed for concentrations of the nutrient or nutrients of
interest. In a simple case, volume changes due to evapotranspiration and
quantities of nutrients withdrawn with the aliquots are small to the point of
being negligible. The slope of concentration (or quantity) with respect to time
is the rate of nutrient uptake, dC/dt, and the rate of nutrient uptake can be
measured for a range of concentrations in a single experiment as the nutrient
concentration is drawn down by plant uptake.
One
of the more interesting methods of generating nutrient uptake data is the
nutrient draw down method of Claasen and Barber (1973). By this method, growing
plants are placed in a limited volume of nutrient solution and are allowed to
draw down the nutrient concentrations over a short period of time. Aliquots are
removed and analyzed for concentrations of the nutrient or nutrients of
interest. In a simple case, volume changes due to evapotranspiration and
quantities of nutrients withdrawn with the aliquots are small to the point of
being negligible. The slope of concentration (or quantity) with respect to time
is the rate of nutrient uptake, dC/dt, and the rate of nutrient uptake can be
measured for a range of concentrations in a single experiment as the nutrient
concentration is drawn down by plant uptake.
 Numerous parameter optimization schemes are known and
computer code is available from Numerical Recipes. Alternatively,
spreadsheets contain such code in the "Optimizer" feature of QuattroPro and the
"Solver" add-in of Excel, and the details of algorithm are not important.
Once the Michaelis-Menten model has been written with a given
set of vmax, Km, and C0 values,
predicted values may be compared to measured values to calculate SSE, and then
Optimizer/Solver may be used to search for and find values of
vmax, Km, and C0 that minimize
SSE. Parameter optimization typically proceeds until either a preset number of
iterations has been completed or continued iterations do not improve the
overall fit by a preset value. The beauty of parameter optimization is that the
initial guesses for the parameter values affect the path of the parameter
search but not the outcome (unless there is a degenerate situation in which the
parameter makes no difference at all in the model.) Sometimes there is need to
constrain values of the parameters to ensure their logical meaning; for
example, Km and C0 must be positive.
Numerous parameter optimization schemes are known and
computer code is available from Numerical Recipes. Alternatively,
spreadsheets contain such code in the "Optimizer" feature of QuattroPro and the
"Solver" add-in of Excel, and the details of algorithm are not important.
Once the Michaelis-Menten model has been written with a given
set of vmax, Km, and C0 values,
predicted values may be compared to measured values to calculate SSE, and then
Optimizer/Solver may be used to search for and find values of
vmax, Km, and C0 that minimize
SSE. Parameter optimization typically proceeds until either a preset number of
iterations has been completed or continued iterations do not improve the
overall fit by a preset value. The beauty of parameter optimization is that the
initial guesses for the parameter values affect the path of the parameter
search but not the outcome (unless there is a degenerate situation in which the
parameter makes no difference at all in the model.) Sometimes there is need to
constrain values of the parameters to ensure their logical meaning; for
example, Km and C0 must be positive.